
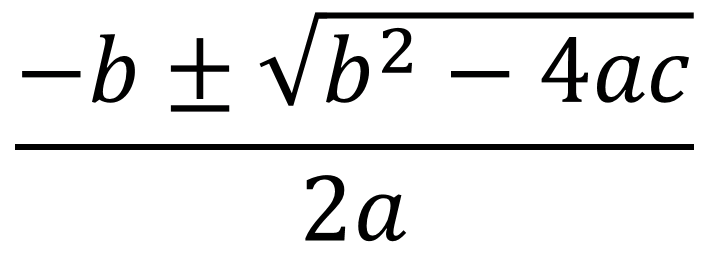
Let us learn in detail the different methods of solving quadratic equations. There are always two solutions to a quadratic equation with either real roots or imaginary roots. Find The Solution To A Quadratic Equation : Example Question 1 1) This is a relatively standard quadratic equation. By completing the square iii) By using quadratic formula i). A quadratic equation is an equation of second degree.Ī quadratic equation makes a \( \cup \)-shaped curve (parabola) if we represent it graphically. There are three methods for solving a quadratic equation: i). The Quadratic Formula Solve 11n2 9n 1 by the quadratic formula. We can write x± a Examples Solve the following quadratic equations. Then the above equation becomes 2x 2 - 3x + 5 0. The solutions to the quadratic equation x25 are 5 and 5, since (5)25 and ( 5)25. The Quadratic Formula A quadratic equation written in standard form, ax2 + bx + c 0, has the solutions. Here is the step-by-step explanation of solving quadratic equations by quadratic formula along with an example where we will be finding the solutions of the quadratic equation 2x 2 3x - 5. If a quadratic polynomial is equated to zero, then we can call it a quadratic equation. The formula is derived from completing the square of a general quadratic equation. When a polynomial is equated to zero, we get a polynomial equation. In this case, the equation does not have real roots.In algebra, polynomials are algebraic expressions with exponents of the variables as whole numbers.

In this case, the equation has one real root. In this case, the equation has two distinct real roots. They are also called ' roots ', or sometimes ' zeros ' There are usually 2 solutions (as shown in this graph). So to solve a quadratic equation using quadratic formula, just get the equation into standard form ax 2 + bx + c 0, and apply the quadratic formula. Because of its importance: $$b² - 4ac$$ is called the determinant of the quadratic equation $$ax² + bx + c = 0$$ The ' solutions ' to the Quadratic Equation are where it is equal to zero. The solutions of a quadratic equation ax 2 + bx + c 0 are given by the quadratic formula x -b (b - 4ac) / (2a). where a and b are called coefficients while c is a constant. This means that every quadratic equation can be put in this form. For a quadratic equation in standard form, these x values will make. The standard form of a quadratic equation is ax2 + bx + c 0. 5x 2 + 12x + 5 5 5x 2 + 12x + 5 - 5 5 - 5. The solutions of a quadratic equation represent the values of x that make the equation true. The expression $$b² - 4ac$$ that appears in the quadratic formula under the square root plays an important role in solving quadratic equations. Solution 2 First, we must turn both quadratic equations in the form ax2 + bx + c 0. The solutions to the quadratic equation, as provided by the Quadratic Formula, are the x-intercepts of the corresponding graphed parabola. The roots x can be found by completing the square, $$ax^2 + bx + c = 0$$ $$x^2 + \frac$$ Quadratic Equation - from Wolfram MathWorld Because it is a second-order polynomial equation, the fundamental theorem of algebra guarantees that it has at least one solution. x-2 or -3 x2+5x+60 x2+2x+3x+60 x(x+2)+3(x+2)0 (x+2)(x+3)0 x-2 or -3.



 0 kommentar(er)
0 kommentar(er)
